On QRAM

In recent years, machine learning has emerged as an area where there are likely to be huge gains from quantum computing. But as a near term application of quantum computing, machine learning algorithms suffer from a major drawback: I/O.

The vast majority of machine learning applications where quantum computing is likely to be required are in situations where there is an absolutely enormous amount of training data. The problem, however, is that no matter how smart you are, you need a way to get that data into your quantum computer. If you are accessing Rigetti’s, IBM’s or Xanadu’s cloud services, the only way for you to get the information into the processor is to encode it in the sequence of gates you apply to the processor. This is a problem. While it might be possible to get a speed-up, reducing the time taken to linear time, this is relatively modest compared to the exponential speed-ups offered by some quantum algorithms. For example, a Gaussian process regression algorithm I worked on scales polylogarithmicly in the size of the input data. The problem is that to reach this kind of performance you need to be able to read the data into the quantum computer in superposition, and this requires new hardware. You won’t be doing this on QX4.

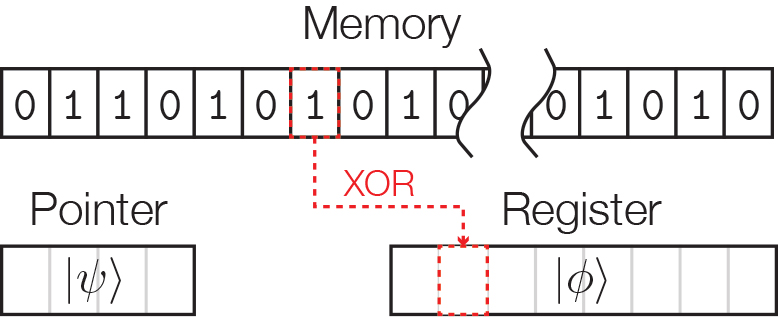
What is required is hardware that accepts a pointer register, which can be in superposition, and returns the classical bit string stored at the location the pointer points to. Since the pointer may be in superposition, this results in a potentially entangled state: \sum_i \alpha_i |i \rangle \to \sum_i \alpha_i |i \rangle | m_i \rangle Generally, we want to make everything reversible, rather than to create new systems out of nowhere, so instead we might write this as \sum_i \alpha_i |i \rangle |x\rangle \to \sum_i \alpha_i |i \rangle | x \oplus m_i \rangle ~.

Is this even possible?

There is a lot of noise generated in the debate over this, and a lot of it comes down to people choosing their own definition of QRAM and then talking at cross purposes. QRAM as described above is simply coherent RAM. It works in basically the same way the RAM in your computer works, with the main difference being that it works in coherent superposition, without dephasing unnecessarily. Imagine cooling your laptop down a lot and then doing everything reversibly. So this should be physically possible. It’s a log depth circuit of Toffoli gates. But this is where we start to go down the rabbit hole.

For whatever reason, there is a section of the community that insists on comparing such a device against a massively parallel classical computer, essentially with the number of cores scaling as the size of the QRAM. I can see the motivation for this, if you start imagining all of your qubits as forming one giant processor, but it makes a number of logical leaps, effectively assuming that your memory is essentially just more processor. You can argue why that might be plausible, but you can also argue against it, and it ignores the comparison that should really be being made: the comparison between a quantum processor with access to QRAM, and a classical RAM model. If you compare like with like, then the power of the quantum version of a RAM model becomes clear.

The other reason for confusion is that sometimes people think of QRAM as shorthand for accomplishing a particular task for which it is frequently used: Given a vector \vec{x}, prepare a pure quantum state |\vec{x}\rangle proportional to \vec{x}. Given access to the QRAM described above storing \vec{x} = \left(x_1,\ldots,x_n\right), there is a relatively simple procedure to do this that succeeds with constant probability most of the time. Basically, you do the following:

• Prepare \frac{1}{\sqrt{n}}\sum_{i=1}^n |i\rangle|0\rangle.
• Query the QRAM to obtain \frac{1}{\sqrt{n}}\sum_{i=1}^n |i\rangle|x_i\rangle
• Add an ancillary qubit and apply a controlled rotation to obtain \frac{1}{\sqrt{n}}\sum_{i=1}^n |i\rangle|x_i\rangle(\sqrt{1-x_i^2}|0\rangle + x_i|1\rangle.
• Measure the ancillary qubit and post-select on measuring “1”, to get something proportional to \sum_{i=1}^n x_i |i\rangle|x_i\rangle.
• Finally call QRAM once more to obtain |\vec{x}\rangle|0\rangle \propto \sum_{i=1}^n x_i |i\rangle|0\rangle.

This works… if your measurement results in “1”. The main issue is the probability with which this happens. It’s constant if the average value of x_i is constant, but in the case where, for example, \vec{x} contains only a single non-zero entry, then it takes O(n) queries to succeed in preparing the state. In fact, you can argue from the search lower bound that at least O(\sqrt{n}) memory queries must be required by -any- procedure to prepare this state.

This use of QRAM is certainly important, but as we show here, you can always prepare in constant time a state that is proportional to a state which close to \vec{x} in the \ell_2 norm, which is sufficient for most applications. Hence we should focus our efforts on building QRAM as initially described above, rather than on building hardware to solve the state preparation problem for arbitrary states. Unfortunately, both functionalities are often referred to as QRAM without distinction, which leads to no end of confusion.

What should we be doing?

One lesson we should learn from the history of computing is that we should learn to walk before we can run. The very first computer memories weren’t like DRAM. They weren’t chips with log depth circuits to select particular memory locations. Rather they were things like sequential mercury delay line memories, and later ferrite core memories which could address a memory essentially quadratically larger than the encoded pointer. Perhaps we can learn something from these early memory architectures?

Before we write them off and insist that medium term quantum computers must not be saddles with sub-optimal memory layouts, it’s worth noting that if we had a quantum equivalent of ferrite-core memories, then we would have quantum machine learning algorithms with runtimes that scaled as the sixth-root of their classical counter parts.